(This is the third in a four-part post that puts 10GB/s in perspective. In the first part, we described what a hypothetical movie-binging robot might be able to do with a 10GB/s SSD. Part 2 defined the standard units of measurements—bits and bytes—used in computer technologies. This section attempts to explain a particularly confusing problem with storage and data: two commonly-used definitions for the same unit prefixes.)
Have you ever purchased a computer system with, say, a 500GB storage device, but when you booted it up for the first time your OS reported only 465GB? We saw in Part 2 that giga- is supposed to mean billion, so a 500GB drive should have a capacity of 500 billion bytes—not 465 billion. Right?
Right!
And not right, too.
If you happened to dig into the discrepancy, you probably realized that the missing 35GB wasn’t missing at all. It’s just that giga- isn’t always used exactly they way you think it should. Just as many bakers consider the word dozen to mean 13, in some circles giga- is used to mean 1,073,741,824! For many of us who grew up understanding that a billion is a 1 with nine 0s following it, this “other” definition may need some clarification.
A Trip Down Memory Lane
Computers use information and instructions contained in data files. These data files reside in two places in a modern computer system: primary memory and secondary storage. Primary memory, now most commonly random access memory (RAM), contains data that computer processors can access immediately. Secondary storage is mainly longer-term storage, such as hard disk drives (HDDs) and solid state drives (SSDs). Data found in secondary storage must first be moved into RAM before a computer can use it. The situation is akin to an office’s desk and its file cabinet: Documents on the office desktop are like files in RAM, as they are the only ones that you—like a computer processor—can access, read, and take action on immediately; you can use documents in the file cabinet, or secondary storage, as well, but only after you get them from the cabinet and put them on the desktop.
The size of a file, wherever it is found, is typically expressed in bytes. And as mentioned in Part 2 of this post, because these sizes typically run in the thousands, millions or even billions of bytes, these sizes are seldom mentioned without special prefixes. The problem arises because manufacturers of secondary storage devices have historically used the traditional set of prefix definitions to measure the storage capacities of their drives, whereas the manufacturers of RAM and CPU chips have chosen to use another set of definitions for the very same prefixes!
A Tale of Two Systems
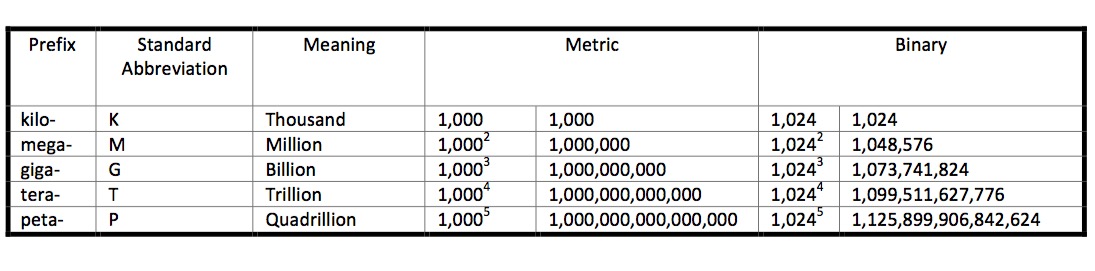
Most computer and electronics industries use the the metric, or decimal, prefix system. Its current form was originally standardized by the International System of Units (SI) in 1960. The metric prefix system has as its base the number 10, so its prefixes correspond to numbers that are integer powers of 10. Kilo-, for example, is 103—which means 10 multiplied by itself three times—or 1,000. Subsequent prefixes in the system can be expressed easily as powers of that 1,000. The prefix mega-, for example, is 1,0002 (1,000,000) and giga- is 1,0003 (1,000,000,000). The storage industry uses the metric prefix system to describe capacity of secondary storage devices.
The binary prefix system comes into play when talking about primary memory. The binary prefix system has as its base the number 2, so its prefixes correspond to numbers that are integer powers of 2. When data gets to primary memory, each piece of information is assigned a unique address that allows the processor to find the data when needed. By the mid-1960s, a binary addressing scheme became standard in computer architectures because a binary system allows for the binary data in memory to be arranged most efficiently such that all have valid addresses.
At first, main memory capacities were expressed in absolute numbers, but when early computer professionals found a need to express larger memory capacities, they also found the need to use prefixes to describe them. The storage industry had already adopted the use of the SI-based metric prefix system. For convenience, these professionals decided to adopt the prefix system, as well…with some modifications. They noticed that the number 1,024, or 210 (binary), was approximately equal to 1,000, or 103 (decimal), so they began using the prefix kilo not to mean 1,000, but to mean 1,024! Subsequent prefixes in the system can be expressed as powers of that 1,024. Mega-, for example, became 1,0242 and giga- became 1,0243.
The following table expands upon a table presented in Part 2 of this post by including not only the meaning of each prefix, but also the exact value of the prefixes of both systems.
One has to remember, however, that the total capacity of our hypothetical SSD is still 500,000,000,000 bytes. It’s just that when you divide this number by a gigabyte, you can have two different values because there are two different definitions of gigabyte. When you define a gigabyte as 1,0003 (or 1,000,000,000) bytes, as the International System of Units and as storage manufactures do, then 500,000,000,000 bytes is the same as 500GB. When you define a gigabyte as 1,0243 (or 1,073,741,824) bytes, as RAM manufacturers and some major operating systems do, then 500,000,000,000 bytes is the same as 465GB.In the early days, this wasn’t a problem—the difference in the approximation was negligible. After all, the discrepancy between a metric kilobyte and a binary kilobyte is only 2.4%. Moreover, anybody who ever talked about KB already knew whether one was talking about 1,000 bytes of storage or 1,024 bytes memory. But as time went on, capacities in both memory and storage started to increase. As capacities grow, the relative differences between the decimal and binary values of the same prefix become more pronounced. For example, although the discrepancy between the binary and metric kilo- might only be 2.4%, the difference between a giga- in the two interpretations grows to 7.4%, and to 12.6% when talking about peta-!
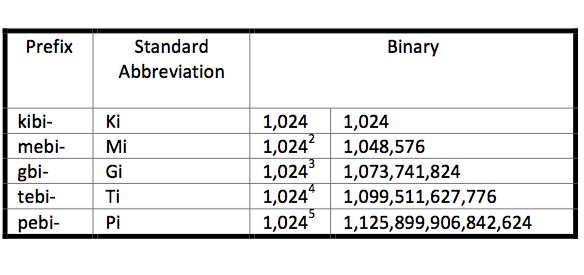
Because of the potential for problems with this discrepancy, a movement in scientific circles began in the late 1990s to formally establish a new, distinct naming convention for prefixes of large binary numbers. In 1998 the resulting binary prefixes were adopted by the standards bodies the International Electrotechnical Commission (IEC), the International Organization for Standardization (ISO), and the National Institute of Standards and Technology (NIST), and are now referred to as “IEC prefixes.” The prefixes in this system are meant to provide obvious distinctions between the two systems and are formed as contractions combining the first two letters of the SI prefixes with the letters bi (short for binary). The following table presents a list of the prefixes and their meanings.
Although the ramifications of mistakenly using one prefix when you are supposed to use the other might not be as dramatic as the disconnect that resulted in the infamous 1999 burn up of NASA’s Mars Climate Orbiter, when its software calculated the force its thrusters in “pounds,” but a separate piece of software took in the data assuming it was in the metric unit “newtons,” understanding the difference between these systems can save you from feeling surprised—or at least from getting confused.Unfortunately, not all computer, software and memory manufacturers have begun using the standardized scientific definitions yet, so you are still likely to see the same prefix used for both metric and binary interpretations. Confusion among consumers can still occur when the storage device they install indicates one capacity using standard prefixes, but their operating system, which may express primary memory and secondary storage capacities in binary prefix terms, displays what looks like a different capacity. Today, to mitigate the confusion, most storage manufacturers include explanations on their products and literature that define the exact value of the prefix they use.
The next part of this post will cover transfer rates and the unique considerations taken in expressing them with data.